Recherche / Research
Here are my main results:
Pénalisées de l'équation des ondes / Penalized Wave Equation
[1] A. Bachelot-Motet, Une estimation a priori sur les solutions de
l'équation des ondes pénalisée, en dimension 1 d'espace. (in French)
[An a priori estimate for the solutions of the penalized problem: ▢ uε=(1/ε)uε-, in one space variable]
C. R. Acad. Sci. Paris Sér. I Math. 299 (1984), no. 14, 659-662.
[2] A. Bachelot-Motet, Une estimation a priori sur les solutions de
l'équation des ondes pénalisée, en dimension 1 et 2 d'espace. (in French)
Proceedings of the 209th EUROMECH Colloquium, 1986, 56-68.
Résonances d'un trou noir de Schwarzschild / Schwarzschild Black-Hole Resonances
[3] A. Bachelot, A. Motet-Bachelot,
Les pôles de résonance de la métrique de Schwarzschild. (in French) [Resonance poles of the Schwarzschild metric]
C. R. Acad. Sci. Paris Sér. I Math. 316 (1993), no. 8, 795–798.
[4] A. Bachelot, A. Motet-Bachelot,
Les résonances d'un trou noir de Schwarzschild. (in French) [The resonances of a Schwarzschild black hole]
Ann. Inst. H. Poincaré Phys. Théor. 59 (1993), no. 1, 3–68. Article in PDF
Abstract. This paper is devoted to the theoretical and computational
investigations of the scattering frequencies of scalar,
electromagnetic, gravitational waves around a spherical Black Hole. We
adopt a time dependent approach: construction of wave operators for the
hyperbolic Regge-Wheeler equation; asymptotic completeness; outgoing
and incoming spectral representations; meromorphic continuation of the
Heisenberg matrix; approximation by dumping and cut-off of the
potentials and interpretation of the semi group Z (t) in the framework
of the Membrane Paradigme. We develop a new procedure for the
computation of the resonances by the spectral analysis of the transient
scattered wave, based on Prony's algorithm.
[5] A. Bachelot, A. Motet-Bachelot,
Resonances of Schwarzschild black holes,
Nonlinear hyperbolic problems: theoretical, applied, and computational aspects (Taormina, 1992), 33–40,
Notes Numer. Fluid Mech., 43, Friedr. Vieweg, Braunschweig, 1993.
[6] A. Motet-Bachelot,
Resonances of the Schwarzschild metric.
Nonlinear evolutionary partial differential equations (Beijing, 1993), 483–487,
AMS/IP Stud. Adv. Math., 3, Amer. Math. Soc., Providence, RI, 1997.
Equation non-linéaire de Dirac en métrique de
Schwarzschild / Nonlinear Dirac Equation in Schwarzschild Metric
[7] A. Bachelot-Motet,
Nonlinear Dirac fields on the Schwarzschild metric,
Classical Quantum Gravity 15 (1998), no. 7, 1815–1825.
We prove the nonexistence on the Schwarzschild metric of particular
stationary states for the nonlinear Dirac equation. In the case where
the Schwarzschild metric is restricted to the exterior of a massive
star, we investigate numerically the existence of such stationary
states with MIT boundary condition.
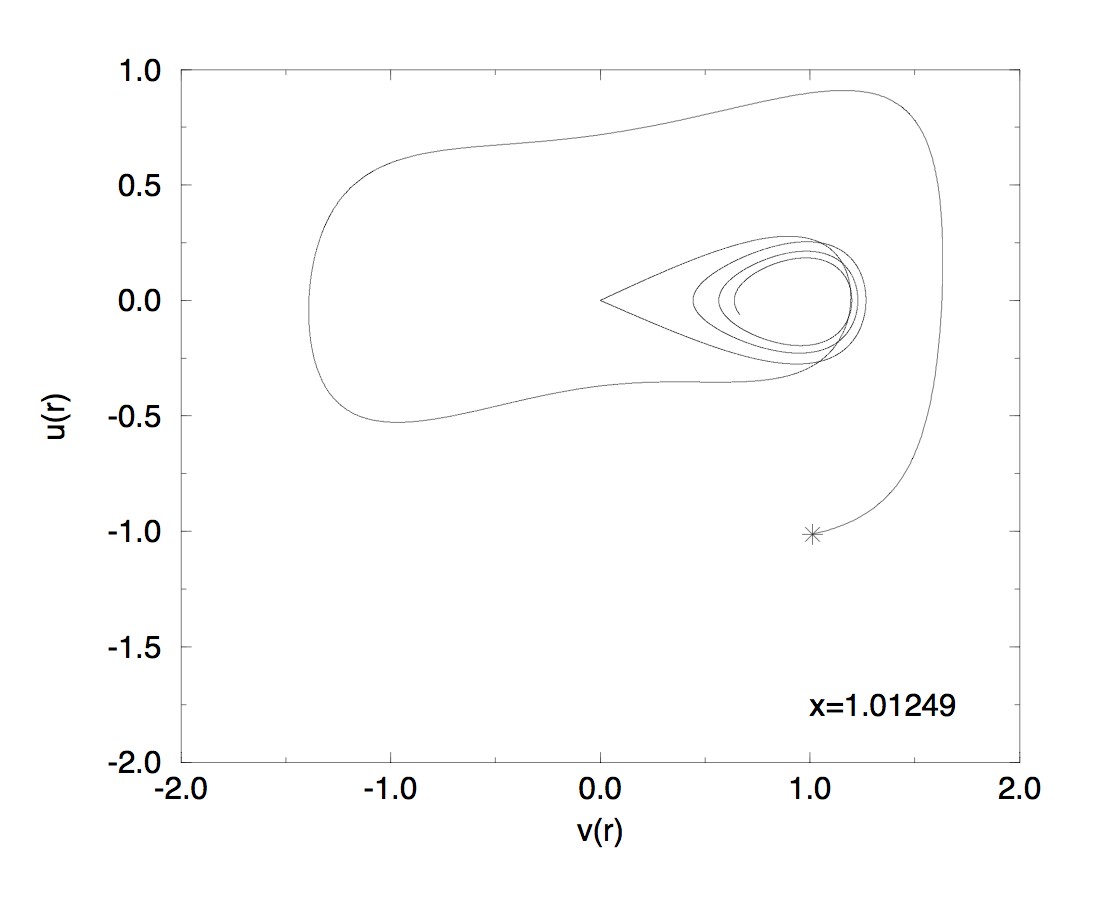
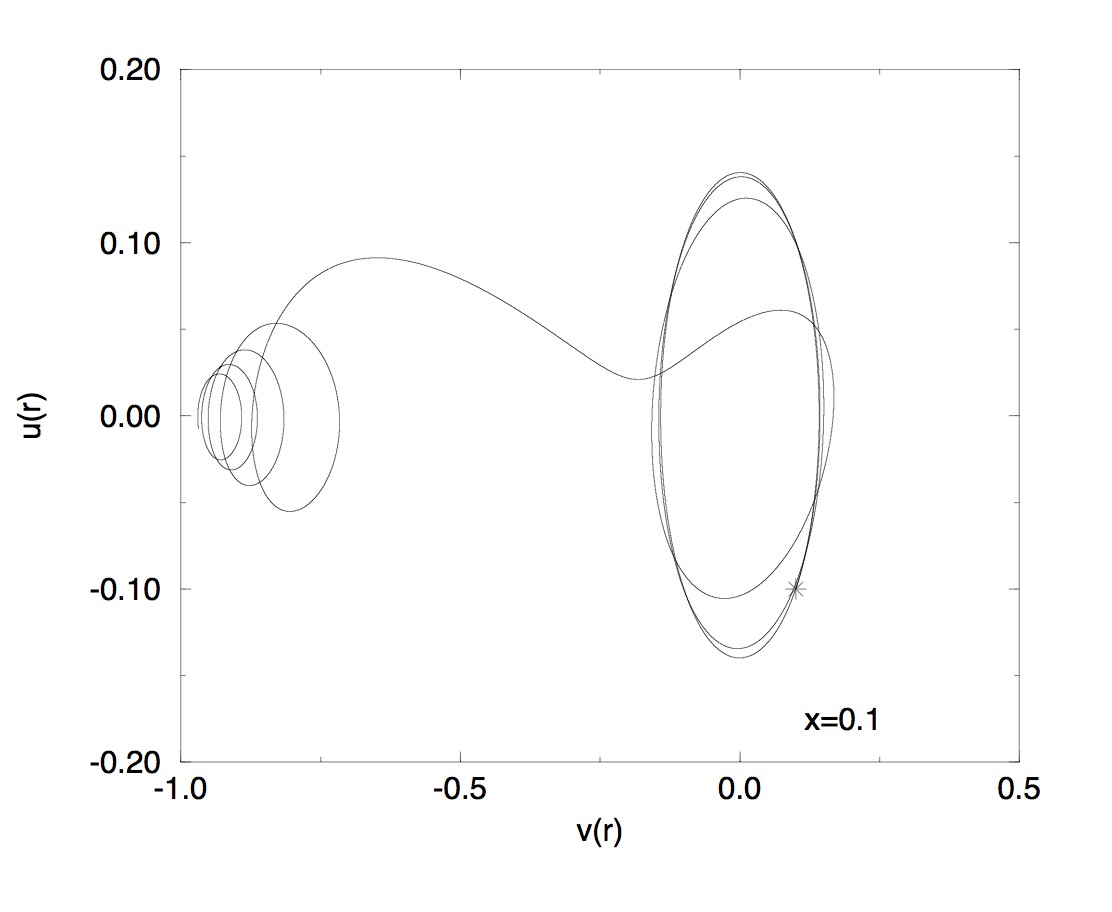
Here are some
stationnary states outside a massive star with the MIT bag condition.
Later, our conjecture has been proved by E. Paturel in his paper: A new
variational principle for a nonlinear Dirac equation on the
Schwarzschild metric, Comm. Math. Phys. 213 (2000), no. 2, 249–266.
Résolution numérique de l'équation des ondes sur
la surface de genre 2 et de courbure constante égale à
-1/ Wave computation on a surface of genus 2 and constant curvature -1
[8] A. Bachelot-Motet, Wave computation on the hyperbolic double doughnut,
J. Comput. Math. 28 (2010), no. 6, 790–806. ARXIV PDF
We compute the waves propagating on the compact surface of constant
negative curvature and genus 2 that is a toy model in quantum chaos
theory and cosmic topology. We adopt a variational approach using
finite elements. We have to implement the action of the fuchsian group
by suitable boundary conditions of periodic type. Despite the
ergodicity of the dynamics that is quantum weak mixing, the computation
is very accurate. A spectral analysis of the transient waves allows to
compute the spectrum and the eigenfunctions of the Laplace-Beltrami
operator. We test the exponential decay due to a localized dumping
satisfying the assumption of geometric control.
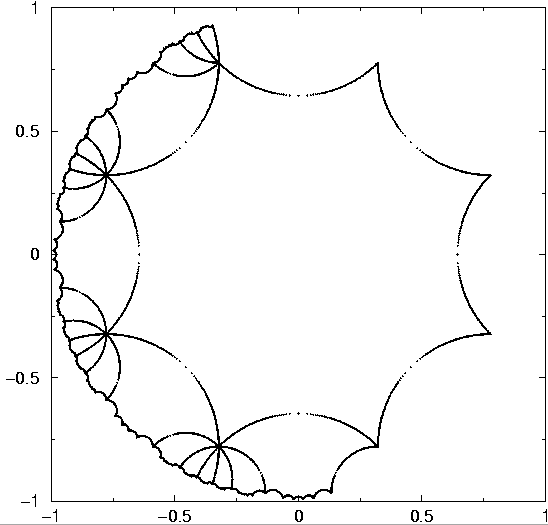
The fundamental domain with a mesh, suitable for the hyperbolic metric.
Visualization of three solutions:
Centered initial data: the solution is symetrical
Occurrence of a chaotic behaviour
Résolution numérique de l'équation des ondes sur l'espace dodécaédrique
de Poincaré / Wave Computation on the Poincaré dodecahedral space.
[9] A. Bachelot-Motet, Wave computation on the Poincaré dodecahedral space,
Classical Quantum Gravity 30 (2013), no. 23, 235010, 31 pp. ARXIV PDF
We
compute the waves propagating on a compact 3-manifold of constant
positive curvature with a non-trivial topology: the Poincaré
dodecahedral space that is a plausible model of multi-connected
universe. We transform the Cauchy problem to a mixed problem posed on a
fundamental domain determined by the quaternionic calculus. We adopt a
variational approach using a space of finite elements that is invariant
under the action of the binary icosahedral group. The computation of
the transient waves is validated with their spectral analysis by
computing a lot of eigenvalues of the Laplace-Beltrami operator.
For some details, see so this page.
Propagation d'ondes dans des univers dodécaèdriques en accélération / Waves on accelerating dodecahedral universes.
[10] A. Bachelot-Motet, A. Bachelot, Waves on accelerating dodecahedral universes,
Classical Quantum Gravity 34 (2017), no. 5, 055010, 39 pp. ARXIV PDF
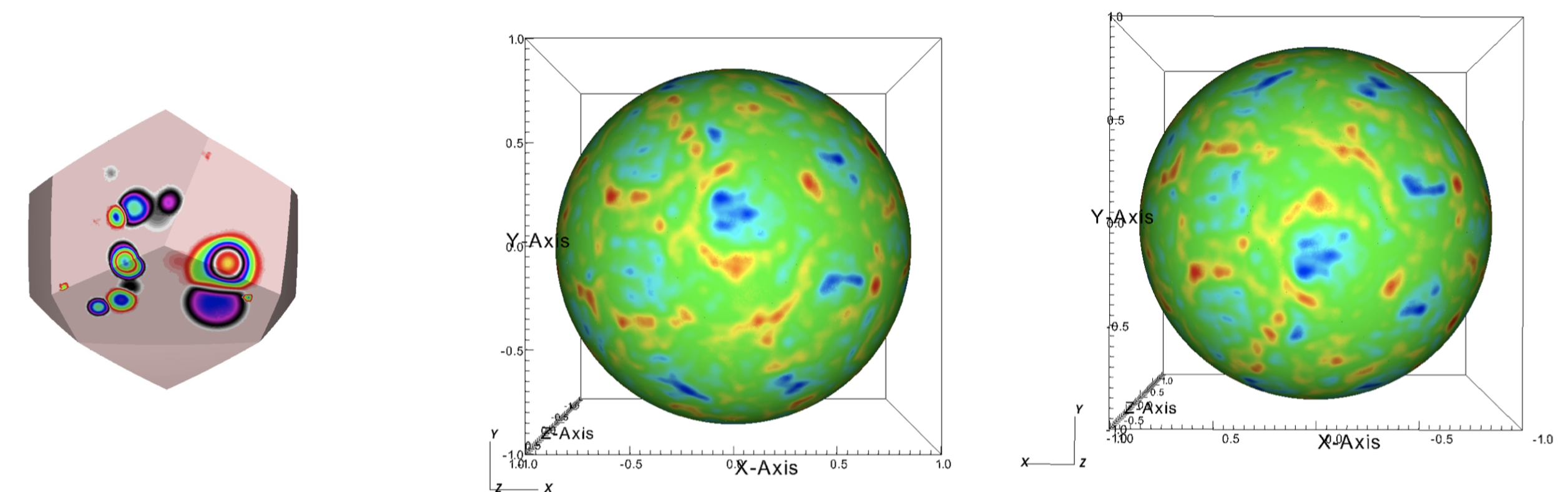
We investigate the wave propagation on a compact 3-manifold of constant
positive curvature with a non trivial topology, the Poincaré
dodecahedral space, when the scale factor is exponentially increasing.
We prove the existence of a limit state as t tends to infinity and we
get its analytic expression. The deep sky is described by this
asymptotic profile thanks to the Sachs-Wolfe formula. We transform the
Cauchy problem into a mixed problem posed on a fundamental domain
determined by the quaternionic calculus. We perform an accurate scheme
of computation: we employ a variational method using a space of second
order finite elements that is invariant under the action of the binary
icosahedral group.
An initial random fluctuation and two antipodal views of the deep sky.
